【LeetCode】102.二叉树的层序遍历

1.问题

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

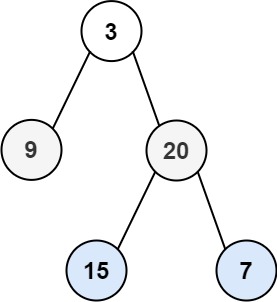
"图1"

示例 1

输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2

输入：root = [1]
输出：[[1]]

示例 3

输入：root = []
输出：[]

提示：

• 树中节点数目在范围 [0, 2000] 内

• -1000 <= Node.val <= 1000

  2.解题思路

  2.1 队列

  二叉树每层的遍历符合队列的特性，必须FIFO(first in first out)，再遍历每层完成后，可以给定一个标记或者层数，表示该层已经遍历完毕，可以将此时的该层遍历结果输出。伪代码：

  //定义队列
  Queue q;
  //结果集
  List res;
  //root 入队
  q.add(root);
  //给定一个标识，标记第一层遍历的结尾
  q.add(null);
  while(q不为空){
  	//出队
  	temp=q.peek();
  	//不是标识的话，入队root.left、root.right
  	if(temp不为null){
  		res.add(temp.val);
  		if(temp.left不为null){
  			q.add(temp.left);
  		}
  		if(temp.right不为null){
  			q.add(temp.right);
  		}
  	}
  	//否则，该层遍历完毕
  	else {
  		q.add(null);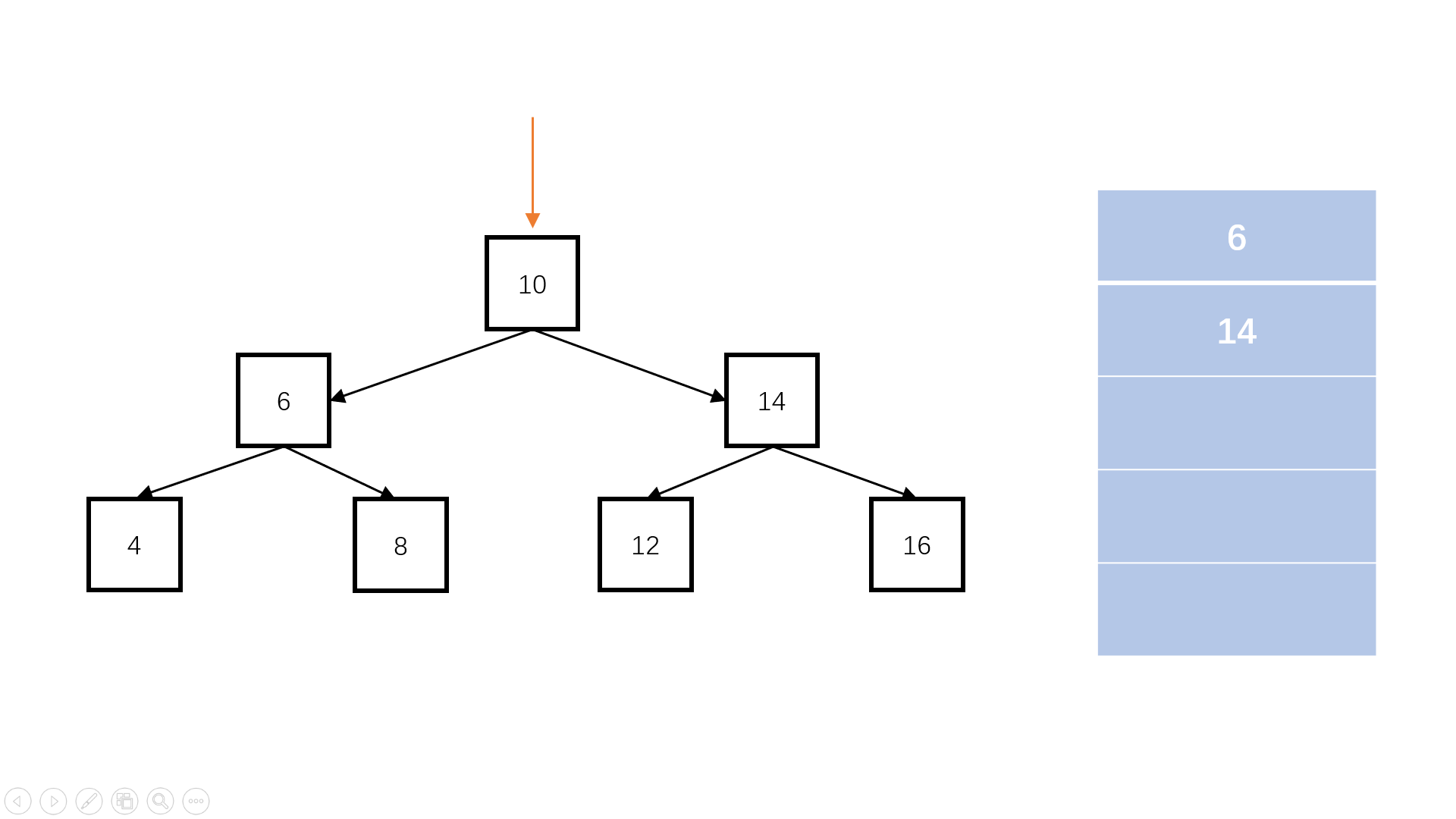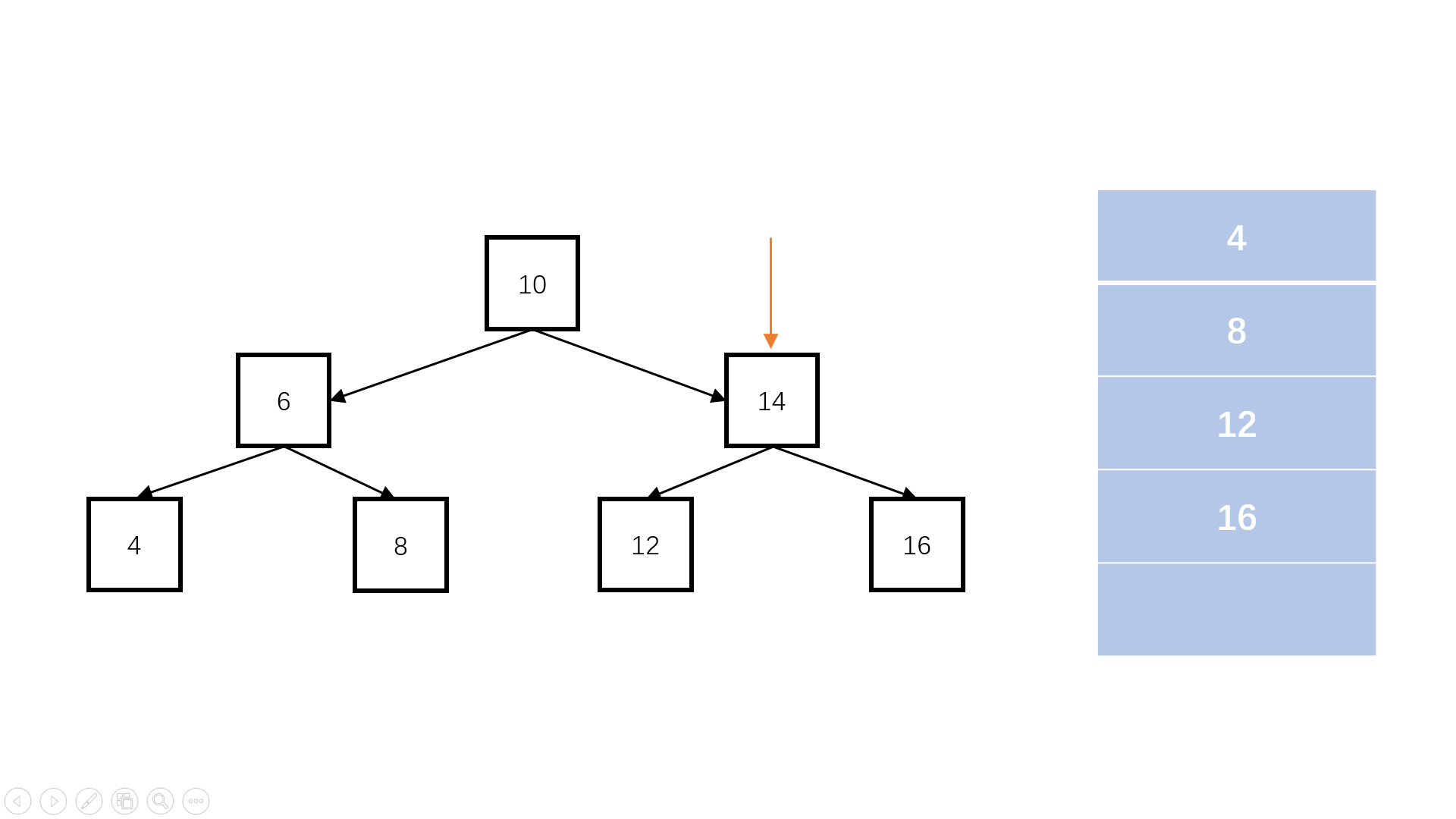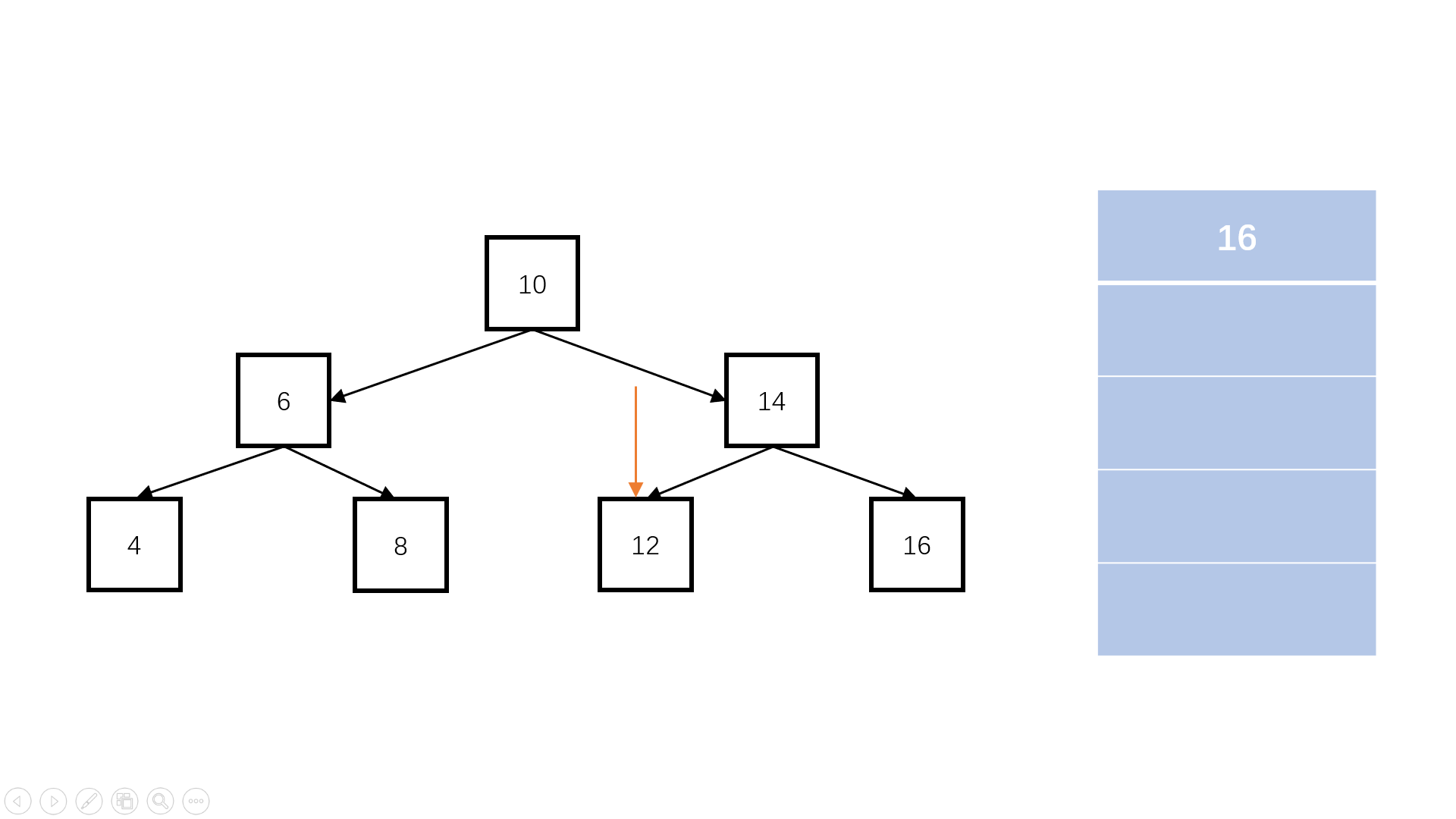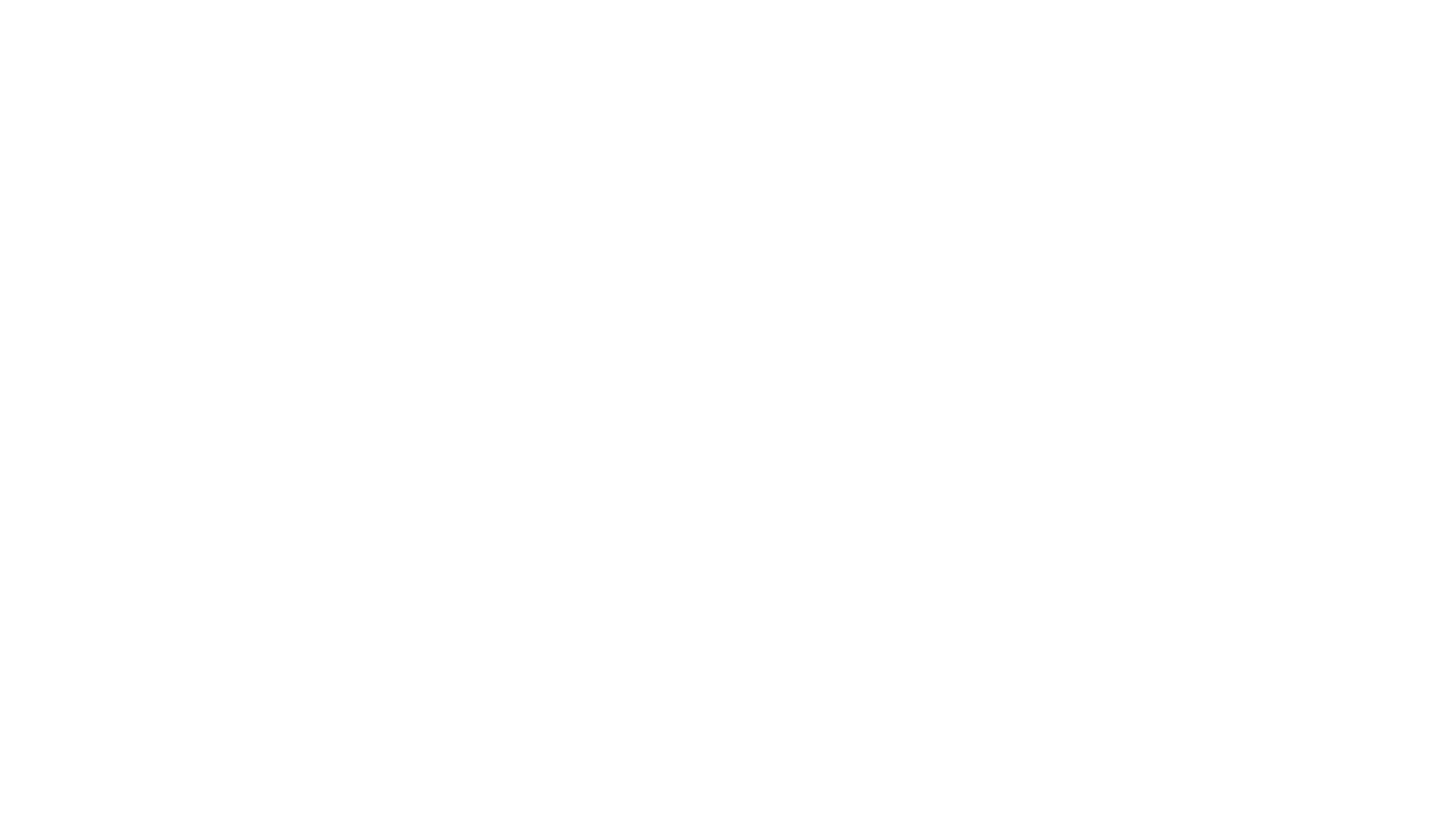
  	}
  }

  
  "图2"

  复杂度分析：

• 时间复杂度：O(n)，其中n为二叉树的节点数，每个节点访问一次

• 空间复杂度：O(n)，队列的空间为二叉树的一层的节点数，最坏情况二叉树的一层为O(n)级

  2.2 递归

  根据二叉树的定义，不难看出，每个节点都有类似的性质。当遍历发生时，对于其左右子树同样适用相同的规则，非常适合递归。可以借鉴之前对于二叉树的前中后序遍历，既然可以用递归解决，那层次遍历也未尝不可。同样可以运用标记的思想，对于同一层，可以标记为相同的深度来进行遍历。伪代码：

  void traverse(TreeNode root, int depth);
  
  //计入子节点，则深度depth+1
  //递归左右时深度记得加1
  traverse(root.left, depth + 1); 
  traverse(root.right, depth + 1);
  
  //每个节点值放入对应的二维数组相应行
  res[depth - 1].push_back(root->val);
  

复杂度分析

• 时间复杂度：O(n)，n为节点数量，DFS对每个节点访问一次，因此递归调用n次，每次调用执行常数次操作，时间复杂度O(n)。
• 空间复杂度：O(n)，空间复杂度在于递归调用深度和每次递归调用辅助空间，辅助空间为常数级，与节点深度相关，当节点深度为n时最大，为O(n)。

  3.代码

  import java.util.*;
  
  /*
   * public class TreeNode {
   *   int val = 0;
   *   TreeNode left = null;
   *   TreeNode right = null;
   * }
   */
  
  public class Solution {
      /**
       * 利用队列的性质
       * @param root TreeNode类
       * @return int整型ArrayList<ArrayList<>>
       */
      public ArrayList<ArrayList<Integer>> levelOrder (TreeNode root) {
          if (null == root) {
              return new ArrayList<>();
          }
          //结果
          ArrayList<ArrayList<Integer>> res = new ArrayList<>();
          //每层临时结果
          ArrayList<Integer> temp = new ArrayList<>();
          TreeNode node;
          //队列
          LinkedList<TreeNode> list = new LinkedList<TreeNode>();
          list.add(root);
          //给定个 层标识
          list.add(null);
          //遍历队列
          while (!list.isEmpty()) {
              node = list.removeFirst();
              if (null != node) {
                  temp.add(node.val);
                  if (null != node.left) {
                      list.add(node.left);
                  }
                  if (null != node.right) {
                      list.add(node.right);
                  }
              }
              //为null节点，说明这一层已经遍历完成
              else {
                  //这里一定要判断下，如果为空，表明二叉树已经遍历完成了
                  if (!temp.isEmpty()) {
                      res.add(temp);
                      temp = new ArrayList<>();
                      list.add(null);
                  }
  
              }
          }
          return res;
      }
  	
  	//记录输出
      ArrayList<ArrayList<Integer> > res = new ArrayList();
      
  	//递归
  	public ArrayList<ArrayList<Integer>> levelOrder (TreeNode root) {
          if(root == null)
              //如果是空，则直接返回
              return res;
          //递归层次遍历
          traverse(root, 0);
          return res;
      }
      
      //临时结果集
      ArrayList<Integer> row;
      
  	void traverse(TreeNode root, int depth) {
          if(root != null){
              //新的一层: 对于二维res来说，将根视为第0层，树的深度正好等于一维res的个数
              if(res.size() == depth){ 
                  row = new ArrayList();
                  res.add(row);
              //读取该层的一维数组，将元素加入末尾
              }else{
                  row = res.get(depth); 
              }
              row.add(root.val);
          }
          else
              return;
          //递归左右时深度记得加1
          traverse(root.left, depth + 1);
          traverse(root.right, depth + 1);
      }
  }